Imagine you have a simplified society split between productive workers and an unproductive group. The unproductive group, forming a fraction r of the population (where 0 < r < 1), demands an income per person equal to a fraction q (where 0 < q < 1) of the average net income per worker (ie the amount of money that a worker will get after transfering money to an unproductive group). The total population is normalized to 1, with workers making up 1 - r. Each worker generates a gross income y > 0, and all societal income comes from workers. Transfers fund the demands, ensuring unproductive income y_u = q * y_w, where y_w is the net (post-transfer) income per worker.
The setup creates an implicit link since demands are based on post-transfer net income.
The main variables are:
Total gross income Y = (1 - r) y.
Let T be the total transfer to the unproductive group. Net income per worker y_w = (Y - T) / (1 - r) = y - T / (1 - r).
The demand gives T = r * y_u = r q y_w.
Solving yields T = (q r y (1 - r)) / (1 - r + q r).
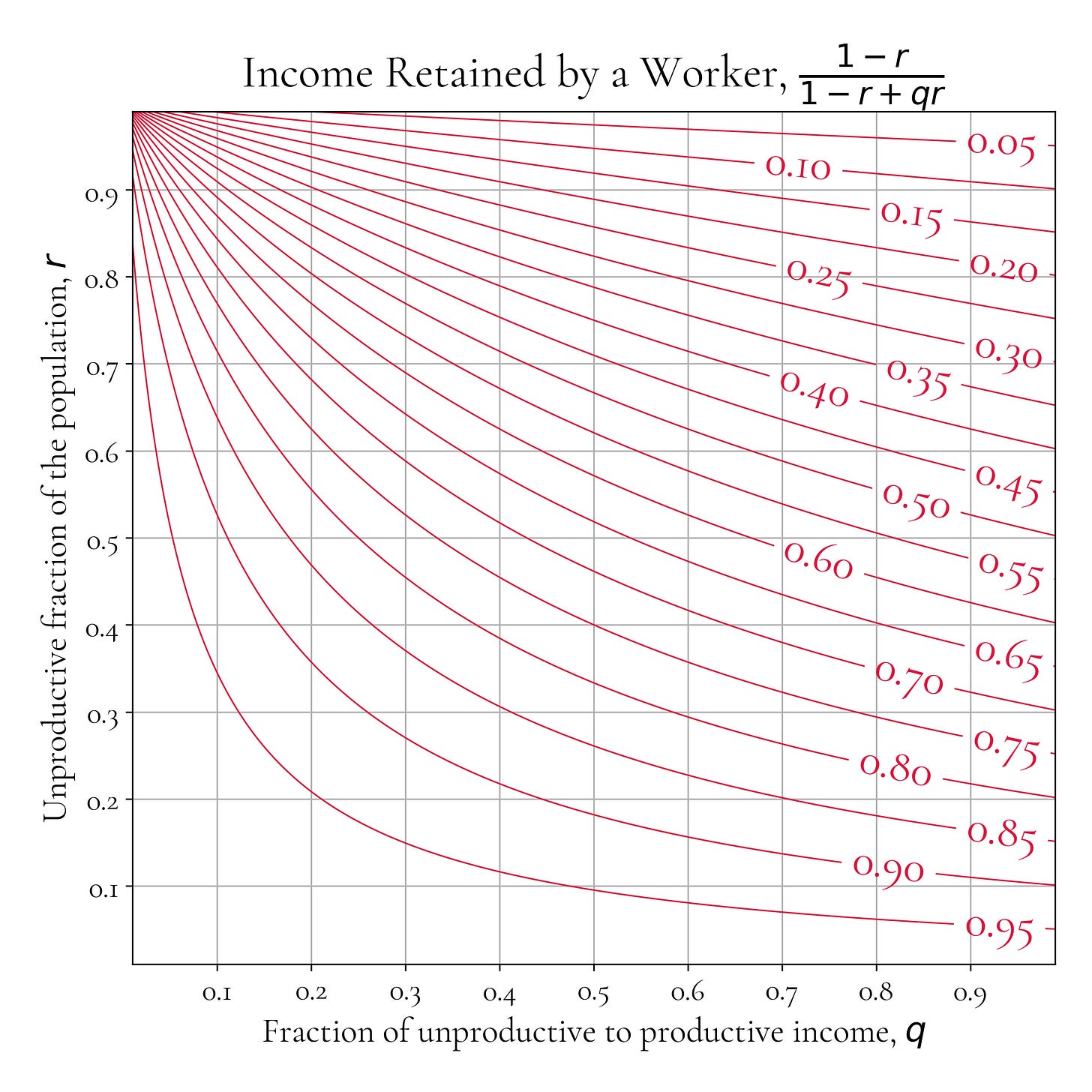
Net income per worker y_w = y (1 - r) / (1 - r + q r).
Income per unproductive person y_u = q y (1 - r) / (1 - r + q r).
Income retained by workers, defined as the fraction of gross income that workers keep after transfers: y_w / y = (1 - r) / (1 - r + q r).